Abstract

This is an experimental project that connects chemistry with abstract mathematics through category theory. At its core lies an original model in which molecules and chemical reactions are represented as objects and morphisms in a multicategory.

The project offers:

• A formal description of chemical reactions as compositional transformations;
• A custom syntax for describing molecules, reactions, and reaction chains;
• A server-side API for analyzing, storing, and searching reaction pathways;
• A possible foundation for synthesis simulation, automatic product derivation, and reaction network visualization.

Why might this be interesting?

• For mathematicians: a living example of applying categorical thinking to natural science.
• For chemists: a tool for analyzing and formalizing reactions without losing chemical meaning.
• For programmers: a clean, extensible project at the intersection of language, graphs, and algebra.

Description

This part is still a work in progress, so the description is not complete. The original work also describes graphs, petri nets, and functors between all these categories.

Category of Molecular Reactions

This is a multicategory \(\mathbf{Mol}\), in which all objects are molecules. These molecules have no names or identifiers within this category — they are abstract molecules. However, for convenience, we will refer to them using familiar names such as \(\mathsf{H_2O}\). Later, when discussing functors, we will treat the names of molecules as a separate structure. So for now, we can say something like:

$$ \mathrm{Ob}(\mathbf{Mol}) = \{ \mathsf{H_2O}, \mathsf{O_2}, \mathsf{NaOH}, \dots \} $$

But you are free to name the molecules however you want — with letters, shapes, or remain purely abstract. For convenience, though, we’ll use familiar chemical names.

Morphisms

Morphisms in this category represent generalized reactions. We are not concerned with the number of molecules involved or the specific type of reaction (e.g., combustion, substitution, oxidation). We focus solely on which molecules can produce which others — the possibility of transformation, not the mechanism. Even if we haven’t discovered a certain reaction yet, we can still operate as if such a transformation exists (via future discoveries or compositions of existing reactions). Just like in \(\mathbf{Set}\), where a transition between sets can be realized through infinitely many possible functions.

Behind these morphisms lies standard chemistry: ordinary reaction equations with the same meaning as functions in \(\mathbf{Set}\).

Let’s look at a few examples.

1. Combustion of Methane (an organic oxidation reaction):

Chemical Equation:

$$ \mathsf{CH_3(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O(g)} $$

Morphisms:

$$ f_1 : (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{CO_2} $$

$$ f_2 : (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{H_2O} $$

Reaction Type: Oxidation (combustion), exothermic.

Explanation: This reaction has two morphisms because it has two products. For compositional clarity, it's better to define two morphisms instead of one with multiple outputs. Also, note that we ignore molecule counts (e.g., we use \(\mathsf{H_2O}\) instead of \(2\mathsf{H_2O}\)). At this level of abstraction, we care only about the presence of transformations.

2. Neutralization: Sodium hydroxide + Hydrochloric acid

Chemical Equation:

$$ \mathsf{NaOH(aq) + HCl(aq) \rightarrow NaCl(aq) + H_2O(l)} $$

Morphisms:

$$ f_1 : (\mathsf{NaOH}, \mathsf{HCl}) \to \mathsf{NaCl} $$

$$ f_2 : (\mathsf{NaOH}, \mathsf{HCl}) \to \mathsf{H_2O} $$

Reaction Type: Double replacement, neutralization, exothermic.

3. Decomposition of Hydrogen Peroxide

Chemical Equation:

$$ \mathsf{2H_2O_2(aq) \rightarrow 2H_2O(l) + O_2(g)} $$

Morphisms:

$$ f_1 : \mathsf{H_2O_2} \to \mathsf{H_2O} $$

$$ f_2 : \mathsf{H_2O_2} \to \mathsf{O_2} $$

Reaction Type: Decomposition, redox.

4. Single Replacement: Zinc + Hydrochloric Acid

Chemical Equation:

$$ \mathsf{Zn(s) + 2HCl(aq) \rightarrow ZnCl_2(aq) + H_2(g)} $$

Morphisms:

$$ f_1 : (\mathsf{Zn}, \mathsf{HCl}) \to \mathsf{ZnCl_2} $$

$$ f_2 : (\mathsf{Zn}, \mathsf{HCl}) \to \mathsf{H_2} $$

Reaction Type: Substitution, redox.

5. Thermal Decomposition of Calcium Carbonate

Chemical Equation:

$$ \mathsf{CaCO_3(s) \xrightarrow{Δ} CaO(s) + CO_2(g)} $$

Morphisms:

$$ f_1 : \mathsf{CaCO_3} \to \mathsf{CaO} $$

$$ f_2 : \mathsf{CaCO_3} \to \mathsf{CO_2} $$

Reaction Type: Decomposition.

Identity Morphisms

Every object has an identity morphism:

$$ \forall o \in \mathrm{Ob}(\mathbf{Mol}) : \mathrm{id}_o \in \mathrm{Hom}_{\mathbf{Mol}}(o, o) $$

For example:

$$ id_{H_2O} : H_2O \to H_2O $$

$$ id_{O_2} : O_2 \to O_2 $$

Usually, this means the molecule is simply at rest, and no reaction occurs. But sometimes it could represent a change in physical state:

$$ \mathsf{Br_{2(g)}} \to \mathsf{Br_{2(l)}} \to \mathsf{Br_{2(s)}} $$

However, since we abstract away from quantities and reaction pathways, and focus only on participants and reaction possibility, we treat it as:

$$ id_{Br_2} : Br_2 \to Br_2 $$

Composition

Let’s say we have a morphism:

$$ f : (A_1, A_2, ..., A_n) \to B $$

And for each \(A_i\), we have a morphism:

$$ g_i : (B_{i1}, ..., B_{im_i}) \to A_i $$

Then we can compose them into:

$$ f \circ (g_1, ..., g_n) : (B_{11}, ..., B_{1m_1}, ..., B_{n1}, ..., B_{nm_n}) \to B $$

Example:

If

\(f: (A, B) \to C\)
\(g: (D, E) \to A\)

Then:

$$ f \circ (g, id_B) : (D, E) \to C $$

Let’s now derive this reaction:

$$ (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{NaOH} $$

Let’s imagine we don't yet know if this is possible, and try to construct it using known reactions.

We start with a known reaction:

$$ \mathsf{Na_2O} + \mathsf{H_2O} \rightarrow \mathsf{2NaOH} $$

This gives us a morphism:

$$ f : (\mathsf{Na_2O}, \mathsf{H_2O}) \to \mathsf{NaOH} $$

Now, we need a way to get \(\mathsf{H_2O}\). One known reaction is:

$$ \mathsf{CH_3(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O(g)} $$

Which gives us:

$$ g : (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{H_2O} $$

So we can form the composition:

$$ f \circ (id_{\mathsf{Na_2O}}, g) : (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{NaOH} $$

Let’s again take the morphism \(f\):

$$ f : (\mathsf{Na_2O}, \ \mathsf{H_2O}) \to \mathsf{NaOH} $$

And think: what other compositions can be constructed? Essentially, the number of such compositions equals the number of ways to obtain \(\mathsf{H_2O}\) \(\times\) the number of ways to obtain \(\mathsf{Na_2O}\). We already know a few ways to derive \(\mathsf{H_2O}\) from the reactions mentioned above:

$$ g_1 : \mathsf{H_2O_2} \to \mathsf{H_2O} $$

$$ g_2 : (\mathsf{NaOH}, \mathsf{HCl}) \to \mathsf{H_2O} $$

$$ g_3 : (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{H_2O} $$

Then:

$$ f \circ (id_{\mathsf{Na_2O}}, g_1) : \mathsf{H_2O_2} \to \mathsf{NaOH} $$

$$ f \circ (id_{\mathsf{Na_2O}}, g_2) : (\mathsf{NaOH}, \mathsf{HCl}) \to \mathsf{NaOH} $$

$$ f \circ (id_{\mathsf{Na_2O}}, g_3) : (\mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{NaOH} $$

Now let’s find ways to produce \(\mathsf{Na_2O}\):

$$ 4\mathsf{Na} + \mathsf{O_2} \rightarrow 2\mathsf{Na_2O} $$

$$ 2\mathsf{Na_2O_2} \xrightarrow{t} 2\mathsf{Na_2O} + \mathsf{O_2} $$

Which give:

$$ h_1 : (\mathsf{Na}, \mathsf{O_2}) \to \mathsf{Na_2O} $$

$$ h_2 : \mathsf{Na_2O_2} \to \mathsf{Na_2O} $$

Now we can compose:

$$ f \circ (h_1, g_1) : (\mathsf{Na}, \mathsf{O_2}, \mathsf{H_2O_2}) \to \mathsf{NaOH} $$

$$ f \circ (h_1, g_2) : (\mathsf{Na}, \mathsf{O_2}, \mathsf{NaOH}, \mathsf{HCl}) \to \mathsf{NaOH} $$

$$ f \circ (h_1, g_3) : (\mathsf{Na}, \mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{NaOH} $$

$$ f \circ (h_2, g_1) : (\mathsf{Na_2O_2}, \mathsf{H_2O_2}) \to \mathsf{NaOH} $$

$$ f \circ (h_2, g_2) : (\mathsf{Na_2O_2}, \mathsf{NaOH}, \mathsf{HCl}) \to \mathsf{NaOH} $$

$$ f \circ (h_2, g_3) : (\mathsf{Na_2O_2}, \mathsf{CH_3}, \mathsf{O_2}) \to \mathsf{NaOH} $$

Let’s now take another look at the morphisms \(h_1\) and \(h_2\):

$$ h_1 : (\mathsf{Na}, \ \mathsf{O_2}) \to \mathsf{Na_2O} $$

$$ h_2 : \mathsf{Na_2O_2} \to \mathsf{Na_2O} $$

Notably, we can produce \(\mathsf{Na_2O_2}\) from \(\mathsf{Na}\) and \(\mathsf{O_2}\) via the following reaction:

$$ \mathsf{2Na + O_2} \to \mathsf{Na_2O_2} $$

This means there exists a morphism:

$$ k: (\mathsf{Na}, \ \mathsf{O_2}) \to \mathsf{Na_2O_2} $$

Which implies that the morphism \(h_1\) can be expressed as the composition:

$$ h_2 \circ k : (\mathsf{Na}, \ \mathsf{O_2}) \to \mathsf{Na_2O} $$

Multifunction to the Category of Sets (\(\mathbf{Mol} \to \mathbf{Set}\))

We define a multifunctor

$$ F : \mathbf{Mol} \to \mathbf{Set} $$

All objects from \(\mathbf{Mol}\) are mapped to singleton sets:

$$ F(\mathsf{H_2O}) = \{ \mathsf{H_2O} \} $$

$$ F(\mathsf{CO_2}) = \{ \mathsf{CO_2} \} $$

$$ \cdots $$

In the category \(\mathbf{Set}\), there always exists a set of all molecules:

$$ K = \bigcup_{m \in \mathrm{Ob}(\mathbf{Mol})} F(m), \quad K \in \mathbf{Set} $$

Each morphism

\(f: (X_1, \dots, X_n) \to Y\) in \(\mathbf{Mol}\) is mapped to a function:

$$ F(f): F(X_1) \times \dots \times F(X_n) \to F(Y) $$

These functions don't contain interesting dynamics, but the functor \(F\) itself allows us to define the set of all molecules \(K\), which can then be used as a basis for further mappings.

$$ \mathsf{H_2O} \in K $$

Note that molecules like \(2H_2O\) do not exist in this set:

$$ \mathsf{2H_2O} \notin K $$

Let’s define the set of all chemical elements \(E\):

$$ E \subset K $$

$$ \mathsf{H} \in E $$

$$ \mathsf{H_2O} \notin E $$

Now we introduce subsets for different categories of elements, such as metals and nonmetals:

• \(NM\): set of nonmetals

$$ NM \subset E $$

$$ \{ \mathsf{H}, \mathsf{C}, \mathsf{N}, \mathsf{O} \} \subset NM $$

• \(HM\): set of metalloids (semi-metals)

$$ HM \subset E $$

• \(M\): set of metals

$$ M \subset E $$

$$ \mathsf{Ti} \in M $$

We assume:

$$ NM \cap M = \emptyset $$

$$ HM \cap M = \emptyset $$

$$ HM \cap NM = \emptyset $$

Metals can also be divided into more specific categories:

• \(M_A\): alkali metals

$$ M_A \subset M $$

$$ \mathsf{Na} \in M_A $$

Alternatively defined as (first group elements excluding hydrogen):

$$ M_A = \{e \in E \mid G(e) = 1\} \setminus \{\mathsf{H}\} = \{ \mathsf{Li}, \mathsf{Na}, \mathsf{K}, \mathsf{Rb}, \mathsf{Cs}, \mathsf{Fr} \} $$

Here, the function \(G\) (described below) maps each element to its group in the periodic table.

• \(M_{AE}\): alkaline earth metals

$$ M_{AE} \subset M $$

$$ M_{AE} = \{ e \in E \mid G(e) = 2 \} = \{ \mathsf{Be}, \mathsf{Mg}, \mathsf{Ca}, \mathsf{Sr}, \mathsf{Ba}, \mathsf{Ra} \} $$

Other metal categories:

• Transition metals: \(M_T \subset M\)
• Lanthanides: \(M_L \subset M\)
• Actinides: \(M_{AC} \subset M\)
• Post-transition metals: \(M_{PT} \subset M\)

Now let’s define sets of aggregate states that a molecule can have:

• Gas form: \(GF\)
• Liquid form: \(LF\)
• Solid form: \(SF\)

$$ GF \subset K \quad ;\quad LF \subset K \quad ; \quad SF \subset K $$

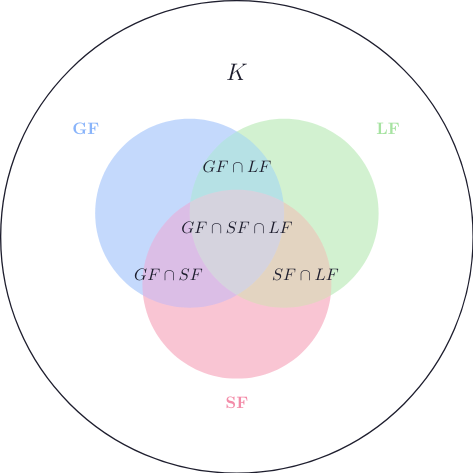
For example, the molecule \(\mathsf{H_2O}\) is in all three subsets:

$$ \mathsf{H_2O} \in GF \cap LF \cap SF $$

Which means that it can exist in all three physical states.

We also define a function that maps each molecule to a tuple of its elements:

$$ \mathbb{E} : K \to \bigcup_{k=1}^\infty E^k $$

Examples:

$$ \mathbb{E}(\mathsf{H_2O}) = (\mathsf{H}, \mathsf{H}, \mathsf{O}) $$

$$ \mathbb{E}(\mathsf{O_2}) = (\mathsf{O}, \mathsf{O}) $$

There’s another version of this function:

$$ \mathbb{E} : \mathcal{P}(K) \to \bigcup_{k=1}^\infty E^k $$

And it can be defined as:

$$ \mathbb{E}(x \in \mathcal{P}(K)) = \bigcup_{k \in x} \mathbb{E}(k) $$

Since objects from \(\mathbf{Mol}\) are mapped to singleton sets (e.g., \(F(H_2O) = \{H_2O\}\)), and those are elements of \(\mathcal{P}(K)\), we can write:

$$ \mathbb{E}(F(\mathsf{H_2O})) = (\mathsf{H}, \mathsf{H}, \mathsf{O}), \quad \mathsf{H_2O} \in \mathbf{Mol} $$

Or:

$$ \mathbb{E}(\{ \mathsf{H_2O}, \mathsf{O_2} \}) = \mathbb{E}(\mathsf{H_2O}) \cup \mathbb{E}(\mathsf{O_2}) = (\mathsf{H}, \mathsf{H}, \mathsf{O}, \mathsf{O}, \mathsf{O}) $$

Molar Mass

We define a function for molar mass:

$$ M : E \to \mathbb{R}^+ $$

Example:

$$ M(\mathsf{O}) = 16 $$

We also define:

$$ M : K \to \mathbb{R}^+ $$

This function is calculated as:

$$ M(k \in K) = \sum_{e \in \mathbb{E}(k)} M(e) $$

Example for \(\mathsf{O_2}\):

$$ M(\mathsf{O_2}) = M(O) + M(O) = 32 $$

And one more variant:

$$ M : \mathcal{P}(K) \to \mathbb{N} $$

$$ M(x \in \mathcal{P}(K)) = \sum_{e \in x} M(e) $$

So we can write:

$$ M(F(\mathsf{O_2})) = M(\mathsf{O}) + M(\mathsf{O}) = 32, \quad \mathsf{O_2} \in \mathbf{Mol} $$

$$ M(\{ \mathsf{H_2O}, \mathsf{O_2} \}) = M(\mathsf{H_2O}) + M(\mathsf{O_2}) = M(\mathsf{H}) + M(\mathsf{H}) + M(\mathsf{O}) + M(\mathsf{O}) + M(\mathsf{O}) = 50 $$

Atomic Number (Number of Protons)

A function assigning the atomic number:

$$ Z : E \to \mathbb{N} $$

$$ Z(\mathsf{N}) = 7 $$

Examples:

$$ \mathsf{O} \mapsto 8, \quad \mathsf{Ni} \mapsto 28, \quad \mathsf{Ti} \mapsto 22, \dots $$

Group Number

Function mapping an element to its group:

$$ G : E \to \mathbb{N} $$

$$ G(\mathsf{Co}) = 9 $$

Period Number

Function mapping an element to its period:

$$ P : E \to \mathbb{N} $$

$$ P(\mathsf{K}) = 4 $$

Relative Atomic Mass

Function for relative atomic mass:

$$ Ar : E \to \mathbb{R}^+ $$

$$ Ar(\mathsf{H}) = 1.008 $$

Mass Number

Function mapping to the mass number:

$$ A : E \to \mathbb{R}^+ $$

Number of Neutrons

Function for computing number of neutrons:

$$ N : E \to \mathbb{R}^+ $$

$$ N(e) = A(e) - Z(e), \quad e \in E $$

Molecule Names

Recall that in \(\mathbf{Mol}\), molecules are unnamed and purely abstract. The names are given separately using the set \(Names\), e.g.:

$$ \mathsf{H_2O} \in Names $$

Even uncommon names like:

$$ \mathsf{OH_2} \in Names $$

We define:

$$ Name : K \to \mathcal{P}(Names) $$

This lets us abstract away from names — so there’s no confusion whether "water" means \(\mathsf{H_2O}\), \(\mathsf{OH_2}\), or both:

$$ Name(▲) = \{ \mathsf{H_2O}, \ \mathsf{OH_2}, \ \dots \} $$

In this case, \(▲\) stands for water as an abstract object — the concept behind the names.

Description

Mol language is a language for describing chemical reactions. If you want to emphasize that the file you have written was written in Mol language, you can add the file extension: example.mol.

Syntax

Writing Molecules

Mol is a case-sensitive language. This means that how you write the names of molecules is very important. The Mol server (which processes Mol code) splits each molecule into atoms and checks whether those atoms are valid (i.e., whether they exist at all). The lexer treats any sequence that starts with an uppercase letter followed by optional lowercase letters as an atom.

Let’s look at the notation 2FeCl3:

• 2: the initial number is completely ignored.
• Fe: this will be recognized as an atom, because it starts with an uppercase letter followed by lowercase letters. If you wrote FE instead, it would be interpreted as two atoms: F and E. But at some point, the server would return an error saying that the atom E does not exist.
• Cl: this will also be interpreted as an atom.
• 3: indicates that there are three Cl atoms in the molecule. This value is taken into account.

Writing Reactions

The syntax of the language is very simple. All reactions can be written in the following format:

List of reactants -> List of products

You can list molecules using either + or ,: NaOH + HCl or NaOH, HCl. You can also use parentheses for clarity: (NaOH + HCl) or (NaOH, HCl). Here’s what a complete reaction might look like:

NaOH + HCl -> H2O

You can also use ; to write multiple reactions in a single line:

NaOH + HCl -> H2O ; CuO + H2 -> Cu + H2O

For convenience, you can use the _ character, which is completely ignored by the language. Here are a few examples: H_2O, H_2_O, K_2SO_4.

Comments

The language supports both block and line comments:

// comment

/*
comment
*/

Example

CH3 + 2O2 -> CO2 + 2H2O ; NaOH + HCl -> NaCl
NaOH + HCl -> H2O

(2H2O2) -> 2H2O + O2


(Zn, HCl) -> ZnCl_2
H2 + Cl2 -> 2HCl
2H2 + O2 -> 2H2O
2Na + Cl2 -> 2NaCl
CaCO3 -> CaO + CO2

// just random comment lol

Fe + S -> FeS
2K + 2H2O -> 2KOH + H2
Zn + 2HCl -> ZnCl2 + H2
CuO + H2 -> Cu + H2O
2Na + 2H2O -> 2NaOH + H2
CaOH2 + CO2 -> CaCO3 + H2O
NH3 + HCl -> NH4Cl
2Fe + 3Cl2 -> 2FeCl3
P + 5Cl2 -> PCl5
3Mg + N2 -> Mg3N2
C + O2 -> CO2
C + O2 -> CO
CO + O2 -> CO2

NaOH + HCl -> NaCl + H2O
H2SO4 + 2KOH -> K2SO4 + 2H2O
NH3 + H2O -> NH4 + OH
CH3COOH + NaOH -> CH3COONa + H2O
H2CO3 + CaOH2 -> CaCO3 + 2H2O
HNO3 + NH3 -> NH4NO3

Zn + CuSO4 -> ZnSO4 + Cu
Fe + CuCl2 -> FeCl2 + Cu

// i don't understand chemistry btw :D

2FeCl3 + H2S -> 2FeCl2 + 2HCl + S
2KMnO4 + 5H2C2O4 + 6H -> 2Mn2 + 10CO2 + 8H2O + 2K
H2O2 + 2KI + H2SO4 -> I2 + 2H2O + K2SO4
2Na + 2H2O -> 2NaOH + H2
Cl2 + 2NaI -> 2NaCl + I2

Commands:

• import - imports a file or stirng of mol code.
• products - outputs products that can be obtained from the provided list of molecules.
• reagents - outputs the reagents needed to obtain the molecule specified in the argument.
• url - displays or edits the current address to the Mol server.
• completions - adds auto-completions to your Shell.

The completions command

The completions command is used to generate auto-completions for some common shells. This means when you type mol in your shell, you can then press your shell’s auto-complete key (usually the Tab key) and it may display what the valid options are, or finish partial input.

The completions first need to be installed for your shell:

# bash
mol completions bash > ~/.local/share/bash-completion/completions/mol

# oh-my-zsh
mol completions zsh > ~/.oh-my-zsh/completions/_mol

autoload -U compinit && compinit

The command prints a completion script for the given shell. Run mol completions --help for a list of supported shells.

Where to place the completions depend on which shell you are using and your operating system. Consult your shell’s documentation for more information one where to place the script.

The url Command

The url command manages the url value in the configuration file located at ~/.config/mol.toml. You can also modify this value manually. The configuration file is created on first launch and contains http://localhost:8080 as the default value, since it's assumed that you'll be running the server manually.

url = "http://localhost:8080"

To check the currently used URL, use the -o flag:

mol url -o

This will simply output the URL: http://localhost:8080.

To set a new value, run the command without any flags and pass the new address:

mol url 'http://localhost:8081'

You can also run mol url --help for a quick usage summary.

The import Command

The import command sends Mol code to the Mol server, after which the server updates the graph of molecular reactions.

Importing a File

You can import files with the .mol extension, as described in the section on the Mol language. To do this, use the -f option:

mol import -f example.mol

Importing a Manually Written String

You can also import Mol code without creating a file:

mol import -s 'CH3 + 2O2 -> CO2 + 2H2O ; NaOH + HCl -> NaCl'

Standard Input

You can also use stdin, which can be useful for scripts:

echo "CH3 + 2O2 -> CO2 + 2H2O ; NaOH + HCl -> NaCl" | mol import

cat example.mol | mol import

You can also combine all methods:

cat example.mol | mol import -f example2.mol -s 'CH3 + 2O2 -> CO2 + 2H2O'

The products Command

The products command displays a list of reactions that are possible using the molecules passed as arguments. Essentially, it means: "show the products I can obtain using these molecules together, assuming I might need one additional component."

In this overview, I’ll be using the example Mol document from earlier sections. Your output may differ if you import more data.

Here’s an example for water:

mol products H2O

Output:

[NH3, H2O] -> OH
[H2O, NH3] -> NH4
[H2O, Na] -> H2
[H2O, Na] -> NaOH
[H2O, K] -> H2
[H2O, K] -> KOH

Here’s another example for sodium:

mol products Na

Output:

[H2O, Na] -> H2
[H2O, Na] -> NaOH
[Cl2, Na] -> NaCl

Some of these reactions also involve water. Let’s try querying the products that can be made from both water and sodium:

mol products Na H2O

Output:

[H2O, Na] -> H2
[H2O, Na] -> NaOH

As you can see, the products command only returns reactions that involve all of the molecules passed as arguments (in this case, H2O and Na). If there were a reaction involving three reactants like H2O + Na + x -> ..., it would also be listed.

The reagents Command

The reagents command displays a list of reactants required to produce the specified molecule passed as an argument. It’s essentially like saying, “give me the reactions that can produce this molecule.”

In this overview, I’ll be using the example Mol document from earlier sections. Your output may differ if you import more data.

Example for water:

mol reagents H2O

Output:

[H2SO4, KI, H2O2] -> H2O
[KMnO4, H, H2C2O4] -> H2O
[H2CO3, CaOH2] -> H2O
[CH3COOH, NaOH] -> H2O
[H2SO4, KOH] -> H2O
[CO2, CaOH2] -> H2O
[CuO, H2] -> H2O
[H2, O2] -> H2O
[H2O2] -> H2O
[NaOH, HCl] -> H2O
[O2, CH3] -> H2O

Example for CO2:

[KMnO4, H2C2O4, H] -> CO2
[O2, CO] -> CO2
[C, O2] -> CO2
[CaCO3] -> CO2
[O2, CH3] -> CO2