Multifunction to the Category of Sets ($\mathbf{Mol} \to \mathbf{Set}$)

We define a multifunctor

$$ F : \mathbf{Mol} \to \mathbf{Set} $$

All objects from $\mathbf{Mol}$ are mapped to singleton sets:

$$ F(\mathsf{H_2O}) = \{ \mathsf{H_2O} \} $$

$$ F(\mathsf{CO_2}) = \{ \mathsf{CO_2} \} $$

$$ \cdots $$

In the category $\mathbf{Set}$, there always exists a set of all molecules:

$$ K = \bigcup_{m \in \mathrm{Ob}(\mathbf{Mol})} F(m), \quad K \in \mathbf{Set} $$

Each morphism

$f: (X_1, \dots, X_n) \to Y$ in $\mathbf{Mol}$ is mapped to a function:

$$ F(f): F(X_1) \times \dots \times F(X_n) \to F(Y) $$

These functions don't contain interesting dynamics, but the functor $F$ itself allows us to define the set of all molecules $K$, which can then be used as a basis for further mappings.

$$ \mathsf{H_2O} \in K $$

Note that molecules like $2H_2O$ do not exist in this set:

$$ \mathsf{2H_2O} \notin K $$

Let’s define the set of all chemical elements $E$:

$$ E \subset K $$

$$ \mathsf{H} \in E $$

$$ \mathsf{H_2O} \notin E $$

Now we introduce subsets for different categories of elements, such as metals and nonmetals:

$NM$: set of nonmetals

$$ NM \subset E $$

$$ \{ \mathsf{H}, \mathsf{C}, \mathsf{N}, \mathsf{O} \} \subset NM $$

$HM$: set of metalloids (semi-metals)

$$ HM \subset E $$

$M$: set of metals

$$ M \subset E $$

$$ \mathsf{Ti} \in M $$

We assume:

$$ NM \cap M = \emptyset $$

$$ HM \cap M = \emptyset $$

$$ HM \cap NM = \emptyset $$

Metals can also be divided into more specific categories:

$M_A$: alkali metals

$$ M_A \subset M $$

$$ \mathsf{Na} \in M_A $$

Alternatively defined as (first group elements excluding hydrogen):

$$ M_A = \{e \in E \mid G(e) = 1\} \setminus \{\mathsf{H}\} = \{ \mathsf{Li}, \mathsf{Na}, \mathsf{K}, \mathsf{Rb}, \mathsf{Cs}, \mathsf{Fr} \} $$

Here, the function $G$ (described below) maps each element to its group in the periodic table.

$M_{AE}$: alkaline earth metals

$$ M_{AE} \subset M $$

$$ M_{AE} = \{ e \in E \mid G(e) = 2 \} = \{ \mathsf{Be}, \mathsf{Mg}, \mathsf{Ca}, \mathsf{Sr}, \mathsf{Ba}, \mathsf{Ra} \} $$

Other metal categories:

Transition metals: $M_T \subset M$
Lanthanides: $M_L \subset M$
Actinides: $M_{AC} \subset M$
Post-transition metals: $M_{PT} \subset M$

Now let’s define sets of aggregate states that a molecule can have:

Gas form: $GF$
Liquid form: $LF$
Solid form: $SF$

$$ GF \subset K \quad ;\quad LF \subset K \quad ; \quad SF \subset K $$

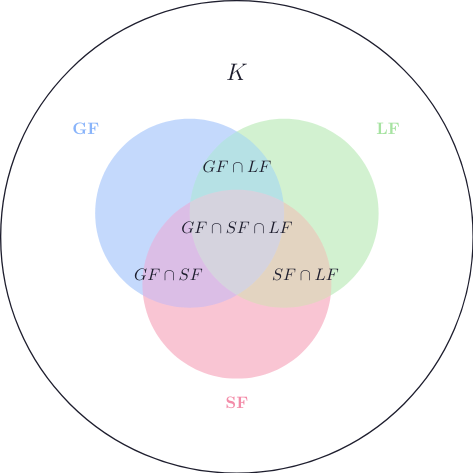
For example, the molecule $\mathsf{H_2O}$ is in all three subsets:

$$ \mathsf{H_2O} \in GF \cap LF \cap SF $$

Which means that it can exist in all three physical states.

We also define a function that maps each molecule to a tuple of its elements:

$$ \mathbb{E} : K \to \bigcup_{k=1}^\infty E^k $$

Examples:

$$ \mathbb{E}(\mathsf{H_2O}) = (\mathsf{H}, \mathsf{H}, \mathsf{O}) $$

$$ \mathbb{E}(\mathsf{O_2}) = (\mathsf{O}, \mathsf{O}) $$

There’s another version of this function:

$$ \mathbb{E} : \mathcal{P}(K) \to \bigcup_{k=1}^\infty E^k $$

And it can be defined as:

$$ \mathbb{E}(x \in \mathcal{P}(K)) = \bigcup_{k \in x} \mathbb{E}(k) $$

Since objects from $\mathbf{Mol}$ are mapped to singleton sets (e.g., $F(H_2O) = \{H_2O\}$), and those are elements of $\mathcal{P}(K)$, we can write:

$$ \mathbb{E}(F(\mathsf{H_2O})) = (\mathsf{H}, \mathsf{H}, \mathsf{O}), \quad \mathsf{H_2O} \in \mathbf{Mol} $$

Or:

$$ \mathbb{E}(\{ \mathsf{H_2O}, \mathsf{O_2} \}) = \mathbb{E}(\mathsf{H_2O}) \cup \mathbb{E}(\mathsf{O_2}) = (\mathsf{H}, \mathsf{H}, \mathsf{O}, \mathsf{O}, \mathsf{O}) $$

Molar Mass

We define a function for molar mass:

$$ M : E \to \mathbb{R}^+ $$

Example:

$$ M(\mathsf{O}) = 16 $$

We also define:

$$ M : K \to \mathbb{R}^+ $$

This function is calculated as:

$$ M(k \in K) = \sum_{e \in \mathbb{E}(k)} M(e) $$

Example for $\mathsf{O_2}$:

$$ M(\mathsf{O_2}) = M(O) + M(O) = 32 $$

And one more variant:

$$ M : \mathcal{P}(K) \to \mathbb{N} $$

$$ M(x \in \mathcal{P}(K)) = \sum_{e \in x} M(e) $$

So we can write:

$$ M(F(\mathsf{O_2})) = M(\mathsf{O}) + M(\mathsf{O}) = 32, \quad \mathsf{O_2} \in \mathbf{Mol} $$

$$ M(\{ \mathsf{H_2O}, \mathsf{O_2} \}) = M(\mathsf{H_2O}) + M(\mathsf{O_2}) = M(\mathsf{H}) + M(\mathsf{H}) + M(\mathsf{O}) + M(\mathsf{O}) + M(\mathsf{O}) = 50 $$