Мультифунктор в категорию множеств (\(\mathbf{Mol} \to \mathbf{Set}\))

$$ F : \mathbf{Mol} \to \mathbf{Set} $$

Все объекты из \(\mathbf{Mol}\) превращаются во множества с одним элементом:

$$ F(\mathsf{H_2O}) = \{\mathsf{H_2O}\} $$

$$ F(\mathsf{CO_2}) = \{\mathsf{CO_2}\} $$

$$ \cdots $$

При этом в категории \(\mathbf{Set}\) всегда есть множество всех молекул:

$$ K = \bigcup_{m \in \mathrm{Ob}(\mathbf{Mol})} F(m), \quad K \in \mathbf{Set} $$

Каждому морфизму \(f: (X_1, \dots, X_n) \to Y\) в \(\mathbf{Mol}\) сопоставляется функция:

$$ F(f): F(X_1) \times \dots \times F(X_n) \to F(Y) $$

Эти функции не несут в себе интересной динамики, однако сам функтор \(F\) позволяет нам определить множество всех молекул \(K\), а также использовать его как основу для дальнейших отображений.

$$ \mathsf{H_2O} \in K $$

При этом там не существует молекулы \(2H_2O\):

$$ \mathsf{2H_2O} \notin K $$

Давайте попробуем описать множество всех химических элементов \(E\):

$$ E \subset K $$

$$ \mathsf{H} \in E $$

$$ \mathsf{H_2O} \notin E $$

Давайте также введем подмножества для разных элементов, например металлов или неметеллов:

• \(NM\) - множество неметаллов:

$$ NM \subset E $$

$$ \{\mathsf{H}, \mathsf{C}, \mathsf{N}, \mathsf{O}\} \subset NM $$

• \(HM\) - множество полуметаллов:

$$ HM \subset E $$

• \(M\) - множество металлов:

$$ M \subset E $$

$$ \mathsf{Ti} \in M $$

При этом:

$$ NM \cap M = \emptyset $$

$$ HM \cap M = \emptyset $$

$$ HM \cap NM = \emptyset $$

При этом это множество можно также разделить на разные типы металлов:

• \(M_{A}\) - Щелочные металлы:

$$ M_A \subset M $$

$$ \mathsf{Na} \in M_{A} $$

Можно еще описать это множество так (все элементы первой группы кроме водорода):

$$ M_A = \{e \in E \mid G(e) = 1\} \setminus \{\mathsf{H}\} = \{\mathsf{Li}, \mathsf{Na}, \mathsf{K}, \mathsf{Rb}, \mathsf{Cs}, \mathsf{Fr}\} $$

Функция \(G\) будет описана чуть ниже. Это такая функция, которая каждому элементу присваивает группу.

• Щелочноземельные металлы(\(M_{AE}\))

$$ M_{AE} \subset M $$

При этом это все элементы второй группы:

$$ M_{AE} = \{e \in E \mid G(e) = 2\} = \{\mathsf{Be}, \mathsf{Mg}, \mathsf{Ca}, \mathsf{Sr}, \mathsf{Ba}, \mathsf{Ra}\} $$

• Переходные металлы (\(M_T\)): \(M_T \subset M\)
• Лантаноиды (\(M_L\)): \(M_L \subset M\)
• Актиноиды (\(M_{AC}\)): \(M_{AC} \subset M\)
• Постпереходные металлы (\(M_{PT}\)): \(M_{PT} \subset M\)

Давайте также опишем множество агрегатных состояний, которые может принимать та или иная молекула:

• Газ \(GF\) (Gas Form)
• Жидкость \(LF\) (Liquid Form)
• Твердое \(SF\) (Solid Form)

$$ GF \subset K \quad ;\quad LF \subset K \quad ; \quad SF \subset K $$

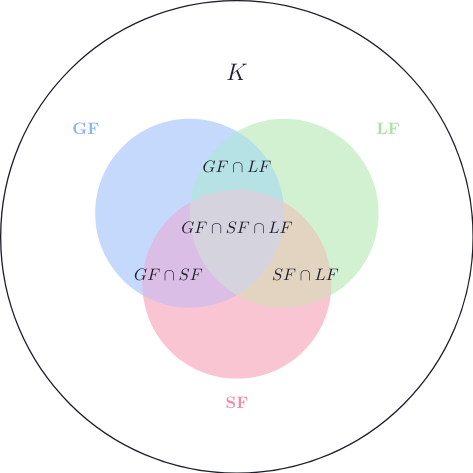
Например, молекула \(\mathsf{H_2O}\) находится во всех трех этих множествах одновременно:

$$ \mathsf{H_2O} \in GF \cap LF \cap SF $$

Что означает, что эта молекула может иметь все три агрегатных состояния.

При этом существует функция, для получения картежа всех элементов, которые находятся в молекуле:

$$ \mathbb{E} : K \to \bigcup_{k=1}^\infty E^k $$

Например:

$$ \mathbb{E}(\mathsf{H_2O}) = (\mathsf{H}, \mathsf{H}, \mathsf{O}) $$

$$ \mathbb{E}(\mathsf{O_2}) = (\mathsf{O}, \mathsf{O}) $$

Также есть еще одна функция с таким же именем:

$$ \mathbb{E} : \mathcal{P}(K) \to \bigcup_{k=1}^\infty E^k $$

Для этой функции даже можно составить реализацию:

$$ \mathbb{E}(x \in \mathcal{P}(K)) = \bigcup_{k \in x} \mathbb{E}(k) $$

Как вы помните, наши объекты из \(\mathbf{Mol}\) переходят во множества с одним элементом (\(F(H_2O) = \{H_2O\}\)). Любое такое множество является элементом множества \(\mathcal{P}(K)\), поэтому возможна запись:

$$ \mathbb{E}(F(\mathsf{H_2O})) = (\mathsf{H}, \mathsf{H}, \mathsf{O}), \quad \mathsf{H_2O} \in \mathbf{Mol} $$

Или даже это:

$$ \mathbb{E}(\{ \mathsf{H_2O}, \ \mathsf{O_2} \}) = \mathbb{E}(\mathsf{H_2O}) \cup \mathbb{E}(\mathsf{O_2}) = (\mathsf{H}, \mathsf{H}, \mathsf{O}, \mathsf{O}, \mathsf{O}) $$

Молярная масса

Давайте введем функцию для нахождения малярной массы:

$$ M: E \to \mathbb{R}^+ $$

Например для элемента \(\mathsf{O}\):

$$ M(\mathsf{O}) = 16 $$

Давайте также введем еще одну функцию:

$$ M : K \to \mathbb{R}^+ $$

При этом у этой функции всегда одна реализация:

$$ M(k\in K) = \sum_{e \in \mathbb{E}(k)}M(e) $$

Для молекулы \(\mathsf{O_2}\):

$$ M(\mathsf{O_2}) = M(O) + M(O) = 32 $$

Также есть еще одна функция:

$$ M : \mathcal{P}(K) \to \mathbb{N} $$ $$ M(x \in \mathcal{P}(K)) = \sum_{e \in x} M(e) $$

С которой возможна такая запись:

$$ M(F(\mathsf{O_2})) = M(\mathsf{O}) + M(\mathsf{O}) = 32, \quad \mathsf{O_2} \in \mathbf{Mol} $$ $$ M(\{\mathsf{H_2O}, \ \mathsf{O_2}\}) = M(\mathsf{H_2O}) + M(\mathsf{O_2}) = M(\mathsf{H}) + M(\mathsf{H}) + M(\mathsf{O}) + M(\mathsf{O}) + M(\mathsf{O}) = 50 $$

Атомный номер (число протонов в ядре атома)

Есть также функция, которая каждому элементу присваивает номер из периодической таблицы:

$$ Z : E \to \mathbb{N} $$

$$ Z(\mathsf{N}) = 7 $$ $$ \mathsf{O} \mapsto 8, \quad \mathsf{Ni} \mapsto 28, \quad \mathsf{Ti} \mapsto 22, \quad \cdots $$

Группа

Есть функция, сопоставляющая каждому элементу группу:

$$ G : E \to \mathbb{N} $$

$$ G(\mathsf{Co}) = 9 $$

Период

Есть функция, сопоставляющая каждому элементу период:

$$ P : E \to \mathbb{N} $$

$$ P(\mathsf{K}) = 4 $$

Относительная атомная масса

Есть функция, сопоставляющая каждому элементу относительную атомную массу:

$$ Ar : E \to \mathbb{R}^+ $$

$$ Ar(\mathsf{H}) = 1,008 $$

Массовое число

Есть функция, сопоставляющая каждому элементу массовое число:

$$ A : E \to \mathbb{R}^+ $$

Число нейтронов

Есть функция, сопоставляющая каждому элементу число нейтронов:

$$ N : E \to \mathbb{R}^+ $$

При этом:

$$ N(\mathsf{e}) = A(\mathsf{e}) - Z(\mathsf{e}), \quad e \in E $$

Имена молекул

Как вы помните в категории \(\mathbf{Mol}\) все молекулы не имеют имен и являются абстрактными молекулами. Имена мы даем отдельно, определяя множество \(Names\):

\(Names\) — это привычные имена молекул на подобии \(\mathsf{H_2O}\):

$$ \mathsf{H_2O} \in Names $$

Там также лежат имена, которые редко используются:

$$ \mathsf{OH_2} \in Names $$

Существует функция:

$$ Name : K \to \mathcal{P}(Names) $$

И теперь мы можем полностью абстрагироваться от названий молекул, чтобы не возникало путаницы, что мы подразумеваем под водой (\(\mathsf{H_2O}\) и / или \(\mathsf{OH_2}\)):

$$ Name(▲) = \{\mathsf{H_2O}, \ \mathsf{OH_2}, \ \dots\} $$

В данном случае \(▲\) — это вода. Мы как-бы берем то, что прячется за словами "вода", "\(\mathsf{H_2O}\)}" или "\(\mathsf{OH_2}\)".